dp进阶
区间dp&树形dp&概率dp&数位dp
前言
今天没有弄题目,就在网上找资料学习和做题。
感觉这一部分好难,不太好理解,难以运用。需要大量的练习。
区间dp
区间类动态规划是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。
令状态 f(i,j) 表示将下标位置 i 到 j 的所有元素合并能获得的价值的最大值,那么 f(i,j)=max{f(i,k)+f(k+1,j)+cost} , cost 为将这两组元素合并起来的代价。
特点
- 合并:将两个或多个部分进行整合,当然也可以反过来。
- 特征:能将问题分解为能两两合并的形式。
- 求解:对整个问题设最优质,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值。
例题
石子合并
题目
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n-1 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n-1 次合并得分总和最小。
输入格式
输入第一行一个整数 n ,表示有 n 堆石子。
第二行 n 个整数,表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
样例
输入
输出
数据范围与提示
对于 100% 的数据,有 1 ≤ n ≤ 200 。
思路
状态转移方程
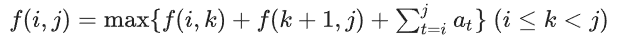
环的处理
将链延长至两倍,变成 2*n 堆,其中第 i 堆与第 n+i 堆相同,用动态规划求解后,取 f(1,n),f(2,n+1),…,f(i,n+i-1) 中的最优值,即为最后的答案。
时间复杂度
O(n³)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
#define Inf 0x3f3f3f3f
using namespace std;
typedef pair<int,int> P;
typedef long long LL;
const int MAXX=210;
const double eps=0.0000001;
int n,a[2*MAXX],sum[2*MAXX],dpmax[2*MAXX][2*MAXX],dpmin[2*MAXX][2*MAXX];
void solve_it(){
scanf("%d",&n);
int n2=n*2;
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
a[n+i]=a[i];
}
for(int i=1;i<=n2;++i)
sum[i]=sum[i-1]+a[i];
memset(dpmin,Inf,sizeof(dpmin));
for(int i=1;i<=n2;++i)
dpmin[i][i]=0;
for(int c=2;c<=n;++c){
for(int i=1;i<n2;++i){
int j=i+c-1;
for(int k=i;k<j&&k<n2;++k){
dpmax[i][j]=max(dpmax[i][j],dpmax[i][k]+dpmax[k+1][j]+sum[j]-sum[i-1]);
dpmin[i][j]=min(dpmin[i][j],dpmin[i][k]+dpmin[k+1][j]+sum[j]-sum[i-1]);
}
}
}
int ansmax=dpmax[1][n],ansmin=dpmin[1][n];
for(int i=2;i<=n;++i){
ansmax=max(ansmax,dpmax[i][i+n-1]);
ansmin=min(ansmin,dpmin[i][i+n-1]);
}
printf("%d\n%d\n",ansmin,ansmax);
}
int main(){
solve_it();
return 0;
}
|
树形dp
就是在树上进行的dp(确信)
例题
没有上司的舞会
题目
某大学有 n 个职员,编号为 1…n 。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 r_i,但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入格式
输入的第一行是一个整数 n。
第 22 到第 (n + 1) 行,每行一个整数,第 (i + 1) 行的整数表示 ii 号职员的快乐指数 r_i 。
第 (n + 2) 到第 2n2n 行,每行输入一对整数 l , k ,代表 k 是 l 的直接上司。
输出格式
输出一行一个整数代表最大的快乐指数。
输入输出样例
输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| 7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
|
输出
数据范围
对于 100% 的数据,保证 1 ≤ n ≤ 6 * 10³ , -128 ≤ r_i ≤ 127 , 1 ≤ l,k ≤ n,且给出的关系一定是一棵树。
思路
用 f(i,0/1) 代表以 i 为根的子树的最优解 (0表示 i 不参加舞会,1表示 i 参加舞会)。
状态转移方程
- f(i,0) = ∑max{f(x,1),f(x,0)} (上司不参加舞会,下属可参加可不参加)
- f(i,1) = ∑f(x,0) + a_i (上司参加舞会,下属不参加)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
#define Inf 0x3f3f3f3f
using namespace std;
typedef pair<int,int> P;
typedef long long LL;
const int MAXX=6005;
const double eps=0.0000001;
int n,a[MAXX],ans[MAXX][2],in[MAXX];
vector<int> son[MAXX];
int dfs(int now,int flag){
if(ans[now][flag]!=Inf)
return ans[now][flag];
if(flag==1){
int re=a[now];
int si=son[now].size();
for(int i=0;i<si;++i)
re+=dfs(son[now][i],0);
return ans[now][flag]=re;
}
else{
int re=0;
int si=son[now].size();
for(int i=0;i<si;++i)
re+=max(dfs(son[now][i],1),dfs(son[now][i],0));
return ans[now][flag]=re;
}
}
void solve_it(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
for(int i=1;i<n;++i){
int jj,kk;scanf("%d%d",&jj,&kk);
son[kk].emplace_back(jj);
in[jj]=1;
}
memset(ans,Inf,sizeof(ans));
int ans=0;
for(int i=1;i<=n;++i){
if(!in[i]){
ans=max(dfs(i,0),dfs(i,1));
}
}
printf("%d\n",ans);
}
int main(){
solve_it();
return 0;
}
|