每日总结-1月17日

2021ACM寒假集训

发布日期: 2022-01-17

文章字数: 1.3k

博弈论

Nim游戏
SG函数
SG定理
mex运算
Wythoff Game

今日战况

Standing

前言

这个博弈论要远比我想象中的复杂，SG函数以及状态转移等等，很是复杂，感觉这部分需要的代码能力非常高，有好多时候，我有点思路，但是我的大脑却不够用，不知道改如何实现这个东西，或者说思考的方向错了。这部分急需大脑

部分题目

E题: 取石子游戏

题目传送门

题目

有两堆石子，数量任意，可以不同。游戏开始由两个人轮流取石子。游戏规定，每次有两种不同的取法，一是可以在任意的一堆中取走任意多的石子；二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目，如果轮到你先取，假设双方都采取最好的策略，问最后你是胜者还是败者。

Input

输入包含若干行，表示若干种石子的初始情况，其中每一行包含两个非负整数a和b，表示两堆石子的数目，a和b都不大于1,000,000,000。

Output

输出对应也有若干行，每行包含一个数字1或0，如果最后你是胜者，则为1，反之，则为0。

Sample Input
1
2
3
2 1
8 4
4 7
Sample Output
1
2
3
0
1
0

思路

这是一个典型的 Wythoff Game ，这里面有一个结论

先手必败当且仅当
$$
abs(a-b)*(1+sqrt{5})/2==min(a,b)
$$
(a,b为两堆石子的石子数量)

即两堆石子数量的差值与黄金分割率的乘积是否与两堆石子数量较小数量相等。

代码

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cmath>
#include<stack>
#include<cstring>
#define Inf 0x3f3f3f3f
using namespace std;
typedef pair<int,int> P;
typedef long long LL;
const int MAXX=205;
const double eps=0.0000001;

int a,s,jj,kk;
double fi=(1.0+sqrt(5.0))*0.5;

void solve_it(){
	while(~scanf("%d%d",&a,&s)){
		jj=min(a,s);kk=max(a,s);
		
		if(jj==(int)(((double)(kk-jj))*fi))
			printf("0\n");
		else
			printf("1\n");
	}
}

int main(){
//	int t;scanf("%d",&t);
//	while(t--)
		solve_it();
	
	return 0;
}

B题: Georgia and Bob

题目传送门

题目

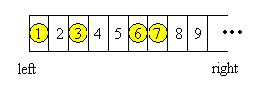
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, …, and place N chessmen on different grids, as shown in the following figure for example:

Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since “Lady first”. Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 … Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, “Georgia will win”, if Georgia will win the game; “Bob will win”, if Bob will win the game; otherwise ‘Not sure’.

Sample Input
1
2
3
4
5
2
3
1 2 3
8
1 5 6 7 9 12 14 17
Sample Output
1
2
Bob will win
Georgia will win

思路

先把棋子升序排列，我们可以将这些棋子两两绑定，如果棋子个数是奇数，那就把第一个和边界绑定，在同一对棋子中，如果对手移动前面那个，那么我们总能移动后面那个相同的距离，相当于移动前面那个将毫无意义，看的是同一对中，后面的那个棋子能移动的距离，即两个棋子之间的距离，谁先把这些距离移动完谁就会赢，这时，这个问题就已经演变成了经典的取石子游戏，直接应用取石子游戏中的结论，所有石子堆的数量的异或值是否为零，为零则先手必败，否则先手必胜。

代码

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cmath>
#include<stack>
#include<cstring>
#define Inf 0x3f3f3f3f
using namespace std;
typedef pair<int,int> P;
typedef long long LL;
const int MAXX=1005;
const double eps=0.0000001;

int n,a[MAXX],s[MAXX];

inline void solve_it(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
		scanf("%d",&a[i]);
	sort(a+1,a+n+1);
	int p=0,pp=0;
	if(n%2)
		s[++p]=a[++pp]-1;
	while(1){
		if(pp>=n) break;
		s[++p]=a[pp+2]-a[pp+1]-1;
		pp+=2;
	}
	int n2=(n+1)/2;
	
	int ans=0;
	for(int i=1;i<=n2;++i)
		ans^=s[i];
	
	if(ans)
		printf("Georgia will win\n");
	else
		printf("Bob will win\n");
}

int main(){
	int t;scanf("%d",&t);
	while(t--)
		solve_it();
	
	return 0;
}