2022杭电多校第3场
contest传送门
战况
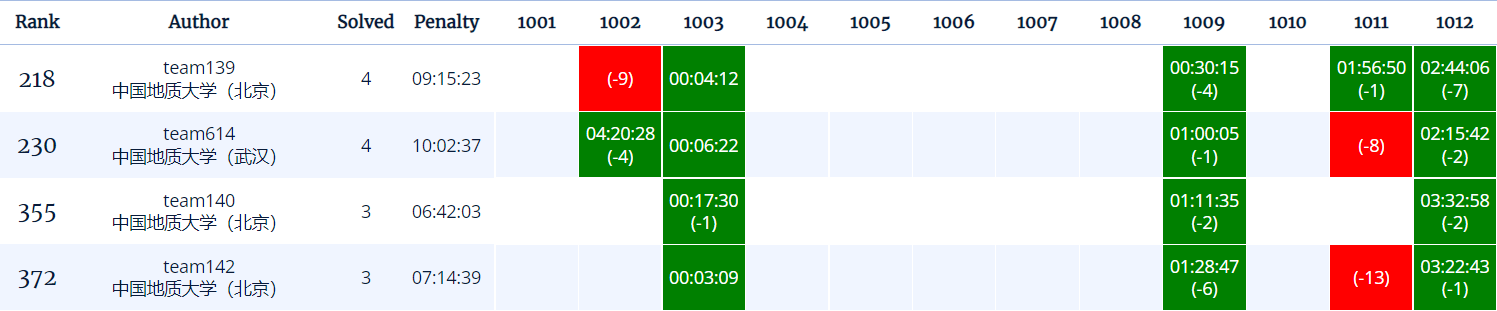
这次的题目确实比前两次要难了不少,过题数量比之前要少。
这次里面没有出字符串题目。
补题
01-Equipment Upgrade
题意
有一把武器需要升级,从 $0$ 级升级到 $n$ 级。
对于当前的等级 $i$ ,花费 $c_i$ 金币进行升级,升级成功的概率是 $p_i$ ,会升级到 $i+1$ 级,也有可能升级失败,之后会有 $(1-p_i)\frac{w_j}{\sum_{k=1}^{i}w_k}$ 的概率变成 $i-j$ 级$(1 \leq j \leq i)$ 。
求从 $0$ 级升级到 $n$ 级所需要的金币的期望。
思路
考虑概率DP, $dp[i]$ 表示从第 $i$ 级升级到第 $n$ 级所需要的金币的期望,显然 $dp[n]=0$ 。
首先根据题目可以写出这样一个式子
$$
dp[i]=p[i]*dp[i+1]+(1-p[i])\frac{\sum_{j=1}^{i}(w[j]*dp[i-j])}{\sum_{k=1}^i w[k]}+c[i]
$$
这个式子比较复杂,无法进行迭代,于是进行化简,
下面把 $\sum_{k=1}^i w[k]$ 记作 $pre[i]$ ,即 $w$ 数组的前缀和,
化简之后得
$$
dp[i]=\frac{dp[i-1]-c[i-1]}{p[i-1]}-\frac{1-p[i-1]}{pre[i-1]*p[i-1]}\sum_{j=1}^{i-1}(w[j]dp[i-1-j])
$$
我们发现这样的形式仍然不好处理,于是我们想到了每一个 $dp[i]$ 都可以使用 $adp[0]+b$ 这样的一个形式来表示,
于是我们可以用两个数组 $a[i],b[i]$ 来辅助表示, $dp[i]=a[i]*dp[0]+b[i]$
这里只把公式推导和思路写出,后面的具体实现需要使用分治+卷积,卷积我还不会,后面的就先不写了
09-Package Delivery
题意
小Q有 $n$ 个包裹,每个包裹有它的存放时间段 $[l[i],r[i]]$ ,暂存点最多可以同时存放 $k$ 个包裹,问小Q最少可以去取多少次包裹
思路
使用优先队列来处理这个区间问题,首先将区间进行排序,之后对于每一个区间,如果当前的 $l[i]$ 大于优先队列顶元素,那么就必须要去取一次包裹,但是也有可能这次取完包裹之后 $l[i]$ 仍然大于优先队列顶元素,需要使用一个 $while$ 循环来进行。遍历结束之后再判断优先队列里面是否还有元素。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
#define Inf 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef pair<int,int> P;
const int MAXX=100005;
int n,k;
P a[MAXX];
priority_queue<int,vector<int>,greater<int> > pq;
inline void solve(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i)
scanf("%d%d",&a[i].first,&a[i].second);
sort(a+1,a+n+1);
int ans=0;
for(int i=1;i<=n;++i){
while(!pq.empty()&&a[i].first>pq.top()){
++ans;
for(int j=1;j<=k;++j){
if(pq.empty()) break;
pq.pop();
}
}
pq.emplace(a[i].second);
}
while(!pq.empty()){
++ans;
for(int j=1;j<=k;++j){
if(pq.empty()) break;
pq.pop();
}
}
printf("%d\n",ans);
}
signed main(){
int t;scanf("%d",&t);
while(t--)
solve();
return 0;
}
|
12-Two Permutations
题意
有两个长度为 $n$ 的排列 $P$ 和 $Q$ ,有一种操作,每一次都取走 $P$ 或 $Q$ 的最左边的数,放到一个新的数组 $R$ 中,直到取完为止。
输入两个长度为 $n$ 的排列 $P$ 和 $Q$ ,一个长度为 $2n$ 的数组 $S$ ,问有多少种取法能否使得组成的 $R$ 和 $S$ 相等。
两种取法不同当且仅当其中有至少一次取的排列不同。(第 $i$ 次取 $P$ 和第 $i$ 次取 $Q$ 即为不同)。
思路
首先要记录一下数组 $S$ 中每个数字的出现次数,特判一下如果有数字的出现次数不是 $2$ ,则直接输出 $0$ 。
我们考虑动态规划,设 $dp[i][j]$ 表示排列 $P$ 的前 $i$ 项都匹配上了 $S$ ,而且 $P_i$ 匹配的是 $S$ 中第 $j$ 次出现 $P_i$ 的情况下的所有方案数。考虑状态转移,对于每一个 $dp[i][j]$ 的状态,我们枚举 $P_{i+1}$ 要匹配 $S$ 中的哪个位置,即匹配第一次出现的那个还是第二次出现的那个,此时,我们必须保证 $P_i$ 匹配的位置与 $P_{i+1}$ 匹配的位置中间的那段连续子序列必须和 $Q$ 中对应的子序列完全匹配。此时,我们考虑使用字符串 $Hash$ 进行 $O(1)$ 判断。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
| #include<bits/stdc++.h>
#define Inf 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef pair<int,int> P;
const int MAXX=300005;
typedef unsigned long long ull;
const LL mod=998244353;
LL n,n2,a[MAXX],s[MAXX],d[2*MAXX],num[MAXX];
ull ncf[2*MAXX],hs[MAXX],hd[2*MAXX],p=233;
LL id[MAXX][2],dp[MAXX][2];
inline void init(){
ncf[0]=1ull;
for(int i=1;i<2*MAXX;++i)
ncf[i]=ncf[i-1]*p;
}
inline ull gethash(ull *h,int l,int r){
return h[r]-h[l-1]*ncf[r-l+1];
}
inline bool check(int ls,int rs,int ld,int rd){
if(ls>rs) return true;
if(ls<1||rs>(int)n||ld<1||rd>(int)n2) return false;
return gethash(hs,ls,rs)==gethash(hd,ld,rd);
}
inline void solve(){
scanf("%lld",&n);n2=n+n;
for(int i=1;i<=n;++i)
scanf("%lld",&a[i]);
for(int i=1;i<=n;++i)
scanf("%lld",&s[i]),hs[i]=hs[i-1]*p+s[i];
for(int i=1;i<=n;++i)
id[i][0]=id[i][1]=0;
for(int i=1;i<=n2;++i){
scanf("%lld",&d[i]);
hd[i]=hd[i-1]*p+d[i];
if(id[d[i]][0])
id[d[i]][1]=i;
else
id[d[i]][0]=i;
}
bool cannot=false;
for(int i=1;i<=n;++i)
if((!id[i][0])||(!id[i][1])){
cannot=true;break;
}
if(cannot){
printf("0\n");
return;
}
for(int i=1;i<=n;++i)
dp[i][0]=dp[i][1]=0LL;
if(check(1,id[a[1]][0]-1,1,id[a[1]][0]-1))
dp[1][0]=1;
if(check(1,id[a[1]][1]-1,1,id[a[1]][1]-1))
dp[1][1]=1;
for(int i=1;i<n;++i)
for(int j=0;j<=1;++j){
if(dp[i][j]){
int jj=id[a[i]][j];
for(int k=0;k<=1;++k){
int kk=id[a[i+1]][k];
if(kk<=jj) continue;
if(check(jj-i+1,kk-i-1,jj+1,kk-1)){
dp[i+1][k]=(dp[i+1][k]+dp[i][j])%mod;
}
}
}
}
LL ans=0;
for(int i=0;i<=1;++i){
if(dp[n][i]){
int jj=id[a[n]][i];
if(check(jj-n+1,n,jj+1,n2))
ans=(ans+dp[n][i])%mod;
}
}
printf("%lld\n",ans);
}
signed main(){
init();
int t;scanf("%d",&t);
while(t--)
solve();
return 0;
}
|
总结
得多练练 $dp$ 了!


